Young's Modulus Of Acrylic

Posted on 22.07.2019

Abs Young's Modulus

Shear modulus
G, S
SI unit	pascal
Derivations from other quantities	G = τ / γ

Use our interactive properties table below to explore by property group, sort, or compare two or more plastic materials. Also, you may want to use our Plastic Material Selection Guide or Interactive Thermoplastics Triangle to assist with the material selection process based on your application requirements. For chemically resistant plastic, view our Chemical Resistance of Plastics chart.

Re: Young's Modulus for Plastic URGENT Pick ten at random and take the average value. Actually, this is a good idea for any engineer, if just to know whether plastics have a typical stiffness of 1kPa, 1MPa, or 1GPa.
The high-impact acrylic resin had a lower elastic modulus (p =.000) and higher flexural strength (p =.001) compared to the traditional acrylic resin. Conclusion Within the limitations of this study, it can be concluded that the high-impact acrylic resin is a suitable denture base material for patients with clinical fracture of the acrylic denture.

Shear strain

In materials science, shear modulus or modulus of rigidity, denoted by G, or sometimes S or μ, is defined as the ratio of shear stress to the shear strain:^[1]

{displaystyle G {stackrel {mathrm {def} }{=}} {frac {tau _{xy}}{gamma _{xy}}}={frac {F/A}{Delta x/l}}={frac {Fl}{ADelta x}}}

where

{displaystyle tau _{xy}=F/A,}

= shear stress

{displaystyle F}

is the force which acts

{displaystyle A}

is the area on which the force acts

{displaystyle gamma _{xy}}

= shear strain. In engineering

{displaystyle :=Delta x/l=tan theta }

, elsewhere

{displaystyle :=theta }

{displaystyle Delta x}

is the transverse displacement

{displaystyle l}

is the initial length

The derived SI unit of shear modulus is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or in thousands of pounds per square inch (ksi). Its dimensional form is M¹L⁻¹T⁻², replacing force by mass times acceleration.

If you wishes to host this document, please ask forpermission by contacting the author first. (but if you're from cheatcc.com,don't bother. Devil May Cry 3 FAQ 2 GamesRadar+Title: Devil May Cry 3 Dante's AwakeningAuthor: OutbreakVersion: 1.3Platform: Sony Playstation 2Game Ver: NTSC/J VersUnpublished work copyright 2003-2005 Outbreak (better known as Xfactor)This FAQ can only be found on the following web-site:can always get the latest version of the document on GameFAQs.If you see this FAQ appearing on any other web site (especially cheatcc.com),please inform the author. You are not allow to take it). Devil may cry 3 secret missions.

3Shear modulus of metals

Explanation[edit]

Material	Typical values for shear modulus (GPa) (at room temperature)
Diamond^[2]	478.0
Steel^[3]	79.3
Iron^[4]	52.5
Copper^[5]	44.7
Titanium^[3]	41.4
Glass^[3]	26.2
Aluminium^[3]	25.5
Polyethylene^[3]	0.117
Rubber^[6]	0.0006

The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law:

Young's modulusE describes the material's strain response to uniaxial stress in the direction of this stress (like pulling on the ends of a wire or putting a weight on top of a column, with the wire getting longer and the column losing height),
the Poisson's ratioν describes the response in the directions orthogonal to this uniaxial stress (the wire getting thinner and the column thicker),
the bulk modulusK describes the material's response to (uniform) hydrostatic pressure (like the pressure at the bottom of the ocean or a deep swimming pool),
the shear modulusG describes the material's response to shear stress (like cutting it with dull scissors).
These moduli are not independent, and for isotropic materials they are connected via the equations ${displaystyle 2G(1+nu )=E=3K(1-2nu )}$ .^[7]

The shear modulus is concerned with the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite face experiences an opposing force (such as friction). In the case of an object shaped like a rectangular prism, it will deform into a parallelepiped. Anisotropic materials such as wood, paper and also essentially all single crystals exhibit differing material response to stress or strain when tested in different directions. In this case, one may need to use the full tensor-expression of the elastic constants, rather than a single scalar value.

One possible definition of a fluid would be a material with zero shear modulus.

Waves[edit]

Influences of selected glass component additions on the shear modulus of a specific base glass.^[8]

In homogeneous and isotropic solids, there are two kinds of waves, pressure waves and shear waves. The velocity of a shear wave, ${displaystyle (v_{s})}$ is controlled by the shear modulus,

{displaystyle v_{s}={sqrt {frac {G}{rho }}}}

where

G is the shear modulus

{displaystyle rho }

is the solid's density.

Shear modulus of metals[edit]

Shear modulus of copper as a function of temperature. The experimental data^[9]^[10] are shown with colored symbols.

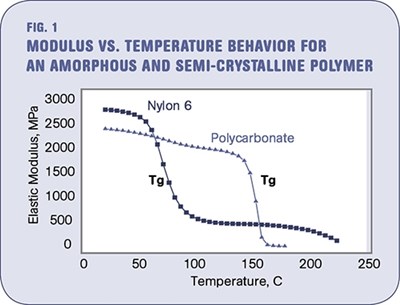
The shear modulus of metals is usually observed to decrease with increasing temperature. At high pressures, the shear modulus also appears to increase with the applied pressure. Correlations between the melting temperature, vacancy formation energy, and the shear modulus have been observed in many metals.^[11]

Several models exist that attempt to predict the shear modulus of metals (and possibly that of alloys). Shear modulus models that have been used in plastic flow computations include:

the MTS shear modulus model developed by^[12] and used in conjunction with the Mechanical Threshold Stress (MTS) plastic flow stress model.^[13]^[14]
the Steinberg-Cochran-Guinan (SCG) shear modulus model developed by^[15] and used in conjunction with the Steinberg-Cochran-Guinan-Lund (SCGL) flow stress model.
the Nadal and LePoac (NP) shear modulus model^[10] that uses Lindemann theory to determine the temperature dependence and the SCG model for pressure dependence of the shear modulus.

MTS shear modulus model[edit]

The MTS shear modulus model has the form:

{displaystyle mu (T)=mu _{0}-{frac {D}{exp(T_{0}/T)-1}}}

where ${displaystyle mu _{0}}$ is the shear modulus at ${displaystyle T=0K}$ , and ${displaystyle D}$ and ${displaystyle T_{0}}$ are material constants.

SCG shear modulus model[edit]

The Steinberg-Cochran-Guinan (SCG) shear modulus model is pressure dependent and has the form

{displaystyle mu (p,T)=mu _{0}+{frac {partial mu }{partial p}}{frac {p}{eta ^{1/3}}}+{frac {partial mu }{partial T}}(T-300);quad eta :=rho /rho _{0}}

where, µ₀ is the shear modulus at the reference state (T = 300 K, p = 0, η = 1), p is the pressure, and T is the temperature.

NP shear modulus model[edit]

The Nadal-Le Poac (NP) shear modulus model is a modified version of the SCG model. The empirical temperature dependence of the shear modulus in the SCG model is replaced with an equation based on Lindemann melting theory. The NP shear modulus model has the form:

{displaystyle mu (p,T)={frac {1}{{mathcal {J}}({hat {T}})}}left[left(mu _{0}+{frac {partial mu }{partial p}}{cfrac {p}{eta ^{1/3}}}right)(1-{hat {T}})+{frac {rho }{Cm}}~k_{b}~Tright];quad C:={cfrac {(6pi ^{2})^{2/3}}{3}}f^{2}}

where

{displaystyle {mathcal {J}}({hat {T}}):=1+exp left[-{cfrac {1+1/zeta }{1+zeta /(1-{hat {T}})}}right]quad {text{for}}quad {hat {T}}:={frac {T}{T_{m}}}in [0,1+zeta ],}

Abs Young's Modulus

and µ₀ is the shear modulus at 0 K and ambient pressure, ζ is a material parameter, k_b is the Boltzmann constant, m is the atomic mass, and f is the Lindemann constant.

References[edit]

^IUPAC, Compendium of Chemical Terminology, 2nd ed. (the 'Gold Book') (1997). Online corrected version: (2006–) 'shear modulus, G'. doi:10.1351/goldbook.S05635
^McSkimin, H.J.; Andreatch, P. (1972). 'Elastic Moduli of Diamond as a Function of Pressure and Temperature'. J. Appl. Phys. 43 (7): 2944–2948. Bibcode:1972JAP..43.2944M. doi:10.1063/1.1661636.
^ ^a^b^c^d^eCrandall, Dahl, Lardner (1959). An Introduction to the Mechanics of Solids. Boston: McGraw-Hill. ISBN0-07-013441-3.CS1 maint: Multiple names: authors list (link)
^Rayne, J.A. (1961). 'Elastic constants of Iron from 4.2 to 300 ° K'. Physical Review. 122 (6): 1714–1716. Bibcode:1961PhRv.122.1714R. doi:10.1103/PhysRev.122.1714.
^Material properties
^Spanos, Pete (2003). 'Cure system effect on low temperature dynamic shear modulus of natural rubber'. Rubber World.
^[Landau LD, Lifshitz EM. Theory of Elasticity, vol. 7. Course of Theoretical Physics. (2nd Ed) Pergamon: Oxford 1970 p13]
^Shear modulus calculation of glasses
^Overton, W.; Gaffney, John (1955). 'Temperature Variation of the Elastic Constants of Cubic Elements. I. Copper'. Physical Review. 98 (4): 969. Bibcode:1955PhRv..98.969O. doi:10.1103/PhysRev.98.969.
^ ^a^bNadal, Marie-Hélène; Le Poac, Philippe (2003). 'Continuous model for the shear modulus as a function of pressure and temperature up to the melting point: Analysis and ultrasonic validation'. Journal of Applied Physics. 93 (5): 2472. Bibcode:2003JAP..93.2472N. doi:10.1063/1.1539913.
^March, N. H., (1996), Electron Correlation in Molecules and Condensed Phases, Springer, ISBN0-306-44844-0 p. 363
^Varshni, Y. (1970). 'Temperature Dependence of the Elastic Constants'. Physical Review B. 2 (10): 3952–3958. Bibcode:1970PhRvB..2.3952V. doi:10.1103/PhysRevB.2.3952.
^Chen, Shuh Rong; Gray, George T. (1996). 'Constitutive behavior of tantalum and tantalum-tungsten alloys'. Metallurgical and Materials Transactions A. 27 (10): 2994. Bibcode:1996MMTA..27.2994C. doi:10.1007/BF02663849.
^Goto, D. M.; Garrett, R. K.; Bingert, J. F.; Chen, S. R.; Gray, G. T. (2000). 'The mechanical threshold stress constitutive-strength model description of HY-100 steel'. Metallurgical and Materials Transactions A. 31 (8): 1985–1996. doi:10.1007/s11661-000-0226-8.
^Guinan, M; Steinberg, D (1974). 'Pressure and temperature derivatives of the isotropic polycrystalline shear modulus for 65 elements'. Journal of Physics and Chemistry of Solids. 35 (11): 1501. Bibcode:1974JPCS..35.1501G. doi:10.1016/S0022-3697(74)80278-7.

Conversion formulae
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas.
${displaystyle K=,}$	${displaystyle E=,}$	${displaystyle lambda =,}$	${displaystyle G=,}$	${displaystyle nu =,}$	${displaystyle M=,}$	Notes
${displaystyle (K,E)}$	${displaystyle {tfrac {3K(3K-E)}{9K-E}}}$	${displaystyle {tfrac {3KE}{9K-E}}}$	${displaystyle {tfrac {3K-E}{6K}}}$	${displaystyle {tfrac {3K(3K+E)}{9K-E}}}$
${displaystyle (K,lambda )}$	${displaystyle {tfrac {9K(K-lambda )}{3K-lambda }}}$	${displaystyle {tfrac {3(K-lambda )}{2}}}$	${displaystyle {tfrac {lambda }{3K-lambda }}}$	${displaystyle 3K-2lambda ,}$
${displaystyle (K,G)}$	${displaystyle {tfrac {9KG}{3K+G}}}$	${displaystyle K-{tfrac {2G}{3}}}$	${displaystyle {tfrac {3K-2G}{2(3K+G)}}}$	${displaystyle K+{tfrac {4G}{3}}}$
${displaystyle (K,nu )}$	${displaystyle 3K(1-2nu ),}$	${displaystyle {tfrac {3Knu }{1+nu }}}$	${displaystyle {tfrac {3K(1-2nu )}{2(1+nu )}}}$	${displaystyle {tfrac {3K(1-nu )}{1+nu }}}$
${displaystyle (K,M)}$	${displaystyle {tfrac {9K(M-K)}{3K+M}}}$	${displaystyle {tfrac {3K-M}{2}}}$	${displaystyle {tfrac {3(M-K)}{4}}}$	${displaystyle {tfrac {3K-M}{3K+M}}}$
${displaystyle (E,lambda )}$	${displaystyle {tfrac {E+3lambda +R}{6}}}$	${displaystyle {tfrac {E-3lambda +R}{4}}}$	${displaystyle {tfrac {2lambda }{E+lambda +R}}}$	${displaystyle {tfrac {E-lambda +R}{2}}}$	${displaystyle R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}}$
${displaystyle (E,G)}$	${displaystyle {tfrac {EG}{3(3G-E)}}}$	${displaystyle {tfrac {G(E-2G)}{3G-E}}}$	${displaystyle {tfrac {E}{2G}}-1}$	${displaystyle {tfrac {G(4G-E)}{3G-E}}}$
${displaystyle (E,nu )}$	${displaystyle {tfrac {E}{3(1-2nu )}}}$	${displaystyle {tfrac {Enu }{(1+nu )(1-2nu )}}}$	${displaystyle {tfrac {E}{2(1+nu )}}}$	${displaystyle {tfrac {E(1-nu )}{(1+nu )(1-2nu )}}}$
${displaystyle (E,M)}$	${displaystyle {tfrac {3M-E+S}{6}}}$	${displaystyle {tfrac {M-E+S}{4}}}$	${displaystyle {tfrac {3M+E-S}{8}}}$	${displaystyle {tfrac {E-M+S}{4M}}}$	${displaystyle S=pm {sqrt {E^{2}+9M^{2}-10EM}}}$ There are two valid solutions. The plus sign leads to ${displaystyle nu geq 0}$ . The minus sign leads to ${displaystyle nu leq 0}$ .
${displaystyle (lambda ,G)}$	${displaystyle lambda +{tfrac {2G}{3}}}$	${displaystyle {tfrac {G(3lambda +2G)}{lambda +G}}}$	${displaystyle {tfrac {lambda }{2(lambda +G)}}}$	${displaystyle lambda +2G,}$
${displaystyle (lambda ,nu )}$	${displaystyle {tfrac {lambda (1+nu )}{3nu }}}$	${displaystyle {tfrac {lambda (1+nu )(1-2nu )}{nu }}}$	${displaystyle {tfrac {lambda (1-2nu )}{2nu }}}$	${displaystyle {tfrac {lambda (1-nu )}{nu }}}$	Cannot be used when ${displaystyle nu =0Leftrightarrow lambda =0}$
${displaystyle (lambda ,M)}$	${displaystyle {tfrac {M+2lambda }{3}}}$	${displaystyle {tfrac {(M-lambda )(M+2lambda )}{M+lambda }}}$	${displaystyle {tfrac {M-lambda }{2}}}$	${displaystyle {tfrac {lambda }{M+lambda }}}$
${displaystyle (G,nu )}$	${displaystyle {tfrac {2G(1+nu )}{3(1-2nu )}}}$	${displaystyle 2G(1+nu ),}$	${displaystyle {tfrac {2Gnu }{1-2nu }}}$	${displaystyle {tfrac {2G(1-nu )}{1-2nu }}}$
${displaystyle (G,M)}$	${displaystyle M-{tfrac {4G}{3}}}$	${displaystyle {tfrac {G(3M-4G)}{M-G}}}$	${displaystyle M-2G,}$	${displaystyle {tfrac {M-2G}{2M-2G}}}$
${displaystyle (nu ,M)}$	${displaystyle {tfrac {M(1+nu )}{3(1-nu )}}}$	${displaystyle {tfrac {M(1+nu )(1-2nu )}{1-nu }}}$	${displaystyle {tfrac {Mnu }{1-nu }}}$	${displaystyle {tfrac {M(1-2nu )}{2(1-nu )}}}$

Retrieved from 'https://en.wikipedia.org/w/index.php?title=Shear_modulus&oldid=904489010'

Explanation[edit]

Waves[edit]

Shear modulus of metals[edit]

MTS shear modulus model[edit]

SCG shear modulus model[edit]

NP shear modulus model[edit]

Abs Young's Modulus

See also[edit]

References[edit]